Our biological aim is to understand collective behavior in biological systems that emerges from the network of interactions between components, as opposed to isolated effects of individual components. Projects involve analysis of high-dimensional & high-throughput data from specific disease contexts and methods development, often for single-cell data.
Dynamical properties of biochemical reaction networks from multiplex and ‘omics data

Multiplex and ‘omics data allow for measuring many of the RNAs, proteins, or other biochemical inside of cells. These high-dimensional datasets reveal rich multivariate relations and emergent properties of the biochemical networks inside cells, which are in principle governed by dynamical principles such as chemical reaction kinetics. We are deriving methods to combine multivariate data analysis methods with dynamical systems analysis of reaction kinetics, to allow for rigorous mechanistic interpretations of data.
Cell states and phenotypes from biochemical states
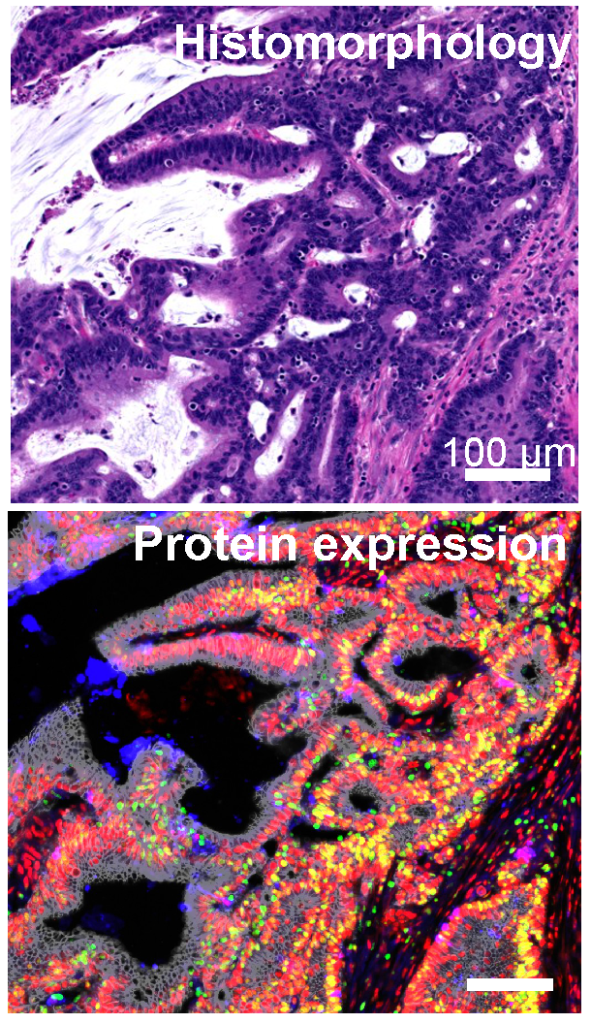
The biochemical state of a cell (e.g. RNA or protein expression profile) are thought to determine the larger scale phenotypes of individual cells or cell populations that eventually emerge. We are investigating the capacity to predict phenotypes (e.g. cell morphology, cycling state, cell type) from high-dimensional biochemical cell states, using both machine learning or first principle derivations.
Spatial interactions and processes in tissue from spatial ‘omics and multiplex data

Spatial ‘omics and single-cell multiplex imaging data not only offer rich high-dimensional information on the biochemical state of cells, but also the spatial patterns that emerge from cell-cell interactions, chemotactic processes, and developmental history. We are both investigating rigorous and informative spatial statistical analysis of such data, as well as how to infer dynamical properties of growth or movement, e.g. as modeled by partial differential equations.
Geometry and topology of biological big data
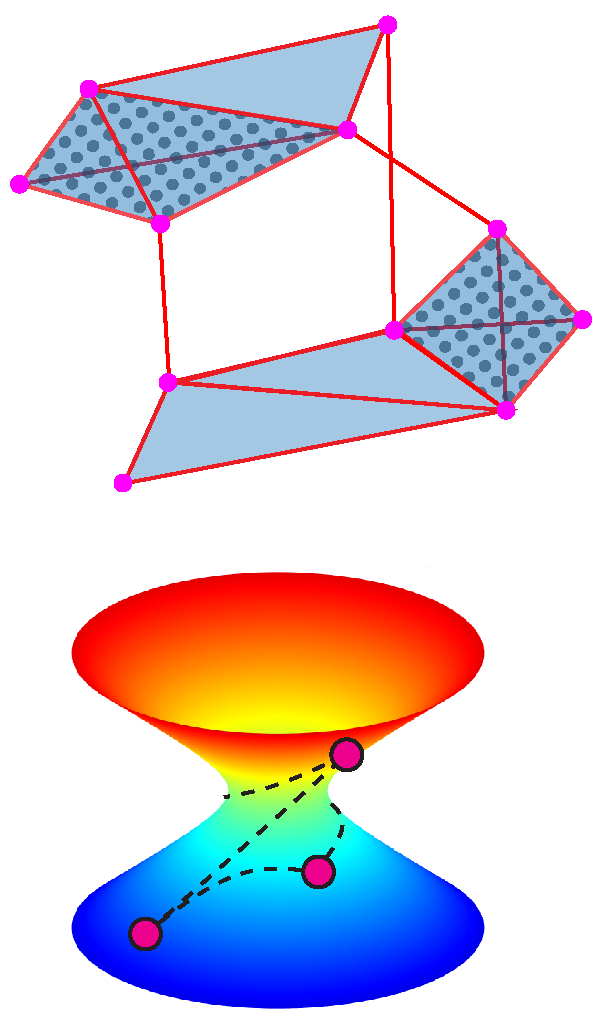
The shape or geometry of data can provide immediate insight into the nature of underlying generative mechanisms. However, the high-dimensional “shape” of big biological data cannot directly be visualized. We are characterizing the geometric traits inherent to high-dimensional biochemical datasets (e.g. single-cell RNAseq) both by using existing mathematical tools such as Topological Data Analysis (TDA), as well as developing ways to characterize data geometry by extending concepts from various subfields of geometry and topology to a data-oriented setting.